Quantum Computing

While enormous advances have been made in computing technologies over the last decades, there are still many computational problems, both in physics and other sciences, that are much too large to solve on a classical computer. In mathematics and computer science, whole clases of problems are well known, for which as the size of the problem grows, the time it sakes to solve the problem increases exponentially with that size. Over the course of the last 20 years or so, there has been a growing interest in the possibility to use the unusual properties of quantum mechanics, which describes the behaviour of microscopic objects, to perform such computations.

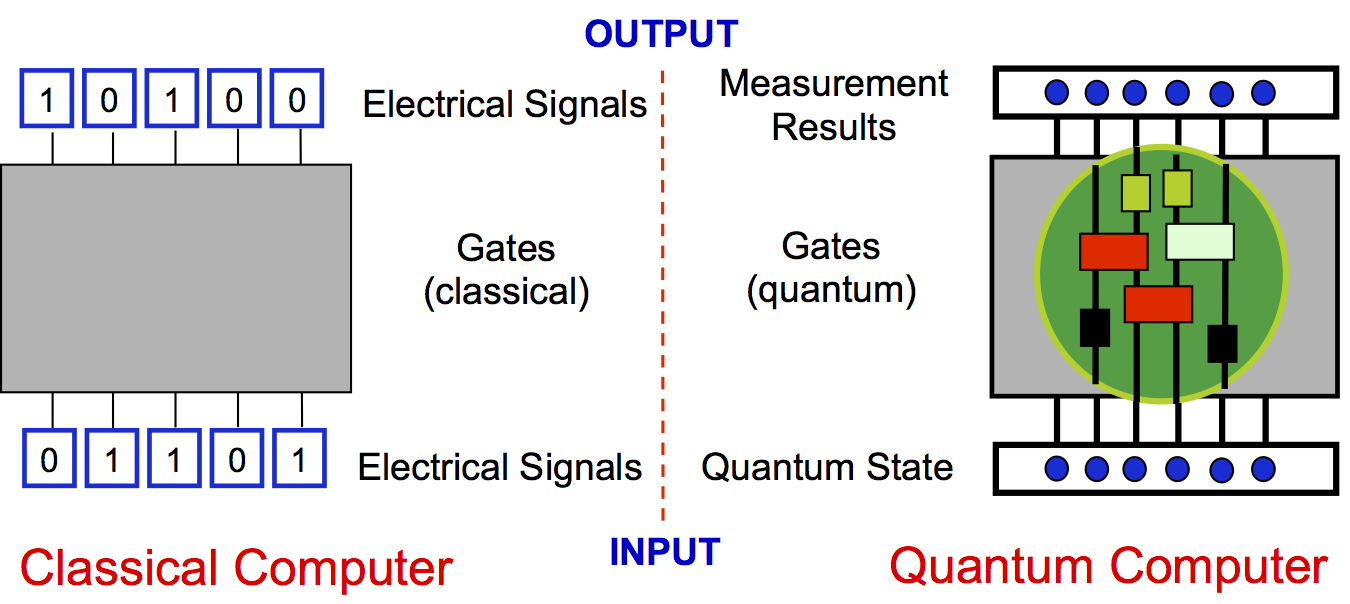
A classical computer takes information, usually as a list of ones and zeros, i.e., bits, (such as electrical signals which can be at two different voltage levels), and uses electronic circuitry to process this information. It performs a set of pre-determined calculations, which can be broken down into so-called "gate operations" in which the state of some bits is changed based on the known value of other bits. The computer then outputs the final result, again as a string of definite ones and zeros. A quantum computer would take information encoded on a quantum state, and then perform pre-determined "gate operations" according to the laws of quantum mechanics, and produce a new quantum state, which can be measured to determine the outcome of the computation.

Qubits, and the power of a quantum computer

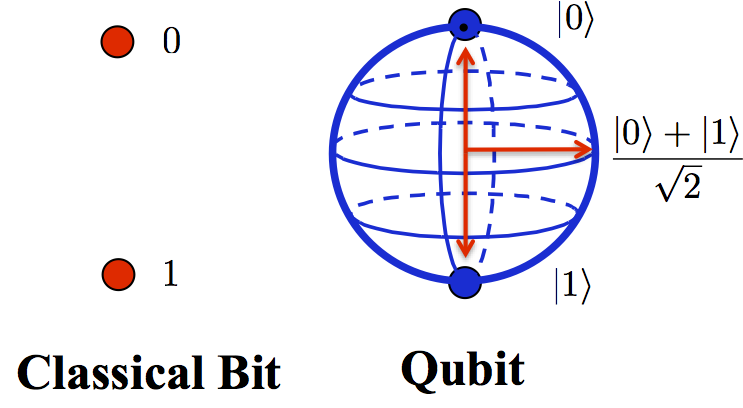
The key difference between the two lies in the ability of a quantum state to represent many possible "classical" states at the same time. Where a classical bit can either be a "0" or a "1", a quantum bit is instead any possible combination or "superposition" of "0" and "1", with complex numbers as coefficients of the superposition. That is, where a "bit" of information in a classical computer can be represented by two points ("0" or "1"), a "qubit" in a quantum computer is instead represented as any point on the surface of a 3D sphere - the "Bloch Sphere". Not only can each qubit be in such a superposition state, but the system as a whole can be in a superposition of every combination of different states of all the qubits. This is why a quantum computer could be so immensely powerful: every possible state could be stored, and processed in parallel with all the others. The number of possible states that can be present in the superposition is huge - if we have N qubits then there are 2N possible states in the superposition. A quantum computer with just 30 qubits would have 1,073,741,824 posible states, and a quantum computer with 300 qubits would have roughly the same number of possible states as the total number of atoms in the known universe.

Quantum algorithms: Programming a quantum computer

There are two difficulties with quantum computers: Determining how to program such a system, and learning how to build one. Programming a quantum computer is made more difficult by the laws of measurement in quantum mechanics: when we measure the system we don't obtain every possible result, but rather the measurement collapses the state onto one useable outcome. Because of this, it isn't easy to design algorithms that make use of the intrinsic power of a quantum computer. They are also difficult to write, because they are mathematically more complex and much less intuitive than algorithms for a classical computer.

The first algorithm for a quantum computer was demonstrated by Peter Shor in 1994, and could be used to find the factors of a number of length n using of the order of log(n) operations. This algorithm makes use of the fact that quantum computers would be good at finding the period of a periodic function, which can be related by number theory to the problem of factorising a number. To give a comparison with classical computers, if we assume that a fast supercomputer would take about a year to factor a 150-digit number, then the same computer would require roughly the lifetime of the universe to factor a 400-digit number. The acceptance that factoring scales like this is the basis of public key encryption systems, which are used every day for secure transactions made over the internet. The security of the system relies on the fact that the "public key", which is a large number, cannot be factored to find the "private key", which is made up of the factors of that number. If a quantum computer could be built that would factor a 150-digit number in a month, then the same quantum computer could factor a 400-digit number in about a year. Of course, this might be bad news for current encryption schemes - but quantum information science also provides new "replacement" encryption schemes to overcome this issue.

Since Shor's algorithm, many new algorithms have been developed, giving significant (though not always exponential) speedups for different problems, including search problems, simulated annealing, and quantum monte-carlo algorithms that would help in determining the properties of certain many-body quantum systems. However, development of such algorithms is still a growing field.

Building a quantum computer

Building a quantum computer is challenging, because it involves manipulating a large number of microscopic objects under the laws of quantum mechanics. However, there are many promising routes to realising a large-scale quantum computer, and much progress has been made in proof-of-principle implementations over the last decade.

The main difficulty is that the microscopic object on which we store each qubit must be isolated from its environment as much as possible to prevent decoherence, where information leaks into the environment. This leaking of information can also be seen as noise from the environment randomising the state of the qubit. Quantum systems are very sensitive to this noise, and such randomisation becomes more difficult to avoid as the system becomes larger.

Examples of systems that are being engineered to implement quantum computing include:

  • Trapped Ions: In these systems, strings of ions are stored in electromagnetic traps, and information is encoded on long-lived internal electronic or nuclear states of the atoms. The information can be manipulated, e.g., using laser coupling and interactions between ions. Coherence times for these systems can extend to many tens of seconds, and recent progress has seen computations with several hundred gate operations performed on up to 14 ions.
  • Neutral Atoms: Atoms are trapped, e.g., in dipole traps generated by laser light, and again information is stored on internal electronic or nuclear states of the atoms and manipulated with laser light and interparticle interactions. Gate operations are typically more difficult to implement in these systems, but trapping techniques such as loading atoms into optical lattice potentials make it easier to create a large register of qubits. These systems are also being used as analogue quantum simulators, which can be seen as a form of special-purpose quantum computer.
  • Superconducting Qubits: These involve circuits of superconducting material, which already have many applications, e.g., in SQUIDs which are used to make sensitive magnetic field measurements. There are various possibilities for encoding qubits in these circuits, including encoding information on the number of superconducting electrons on a separated island in the circuit (charge qubit), on the direction of a current and related magnetic field through a loop (flux qubit) or in oscillatory states current states (phase qubit). The information can be manipulated, e.g., using microwave pulses, and magnetic field coupling of different qubits. These systems have a natural speed advantage over ions and atoms, but are more difficult to fabricate in large coupled arrays.
There are also many other candidates for qubits, including electron spins in solid-state systems such as quantum dots, colour centres in diamond, optical photons, and nuclear spin states manipulated with NMR techniques.

Further reading:

Note: Some journal articles listed above require a subscription. The arxiv references should be available from any location without such subscriptions.

Return to research summary page